10.6.2 Statistische
Methoden
10.6.2.1 Rechengrößen
Wenn man zur Überprüfung von vielen
Teilen eine Stichprobe zieht, erhält man eine endliche
Anzahl von Messwerten. Mit ausreichend vielen Messwerten kann
man einen stetigen Kurvenverlauf zeichnen, der die Grundgesamtheit
der Teile widerspiegelt, d. h. aller Teile, auch derjenigen,
die nicht gemessen wurden.
Verteilungen unterscheiden sich in ihrem Kurvenverlauf hinsichtlich
Lage, Breite und Form, die auch nebeneinander auftreten und
sich überlagern können. Sehr häufig gehorchen
Messwerte der Normalverteilung, auch Gauß´sche
Verteilung oder, wegen ihrer Form, Glockenkurve
genannt.
Die Normalverteilung wird die durch zwei folgenden Kennwerte
mathematisch beschrieben.
Arithmetischer Mittelwert:
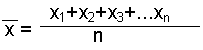
mit n = Anzahl der Messwerte und mit den Einzelwerten Xi von
X1 bis Xn
Standardabweichung:
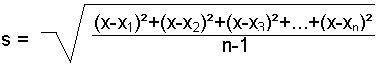
Der Mittelwert x ist die Mitte der Normalverteilungskurve
und kennzeichnet die Lage der Verteilung.
Die Standardabweichung s beschreibt die Streuung des Prozesses,
sie ist ein Maß für die Breite einer Normalverteilungskurve
und ist geometrisch der Abstand zwischen Mittelwert x und
dem Wendepunkt der Normalverteilung.
Die Fläche unterhalb der Normalverteilungskurve entspricht
der Häufigkeit des Vorkommens von Messwerten. Im Bereich
± 1 s um den Mittelwert x, also 2 s, entspricht die
schraffierte Fläche unterhalb der Normalverteilungskurve
68,26 % aller Werte. Im Bereich ± 3 s um den Mittelwert,
also 6 s, sind es 99,73 % aller Werte. Man definiert den Abstand
von 3 s zum Mittelwert als natürliche Prozessgrenzen.
|
|

